
Harmonic Oscillator Wave Function Normalization. V x V0 x x V x x x 1 2 x x 2 2V x2. Because of the association of the wavefunction with a probability density it is necessary for the wavefunction to include a normalization constant Nv. In order to introduce the notion of wave function for the classical harmonic oscillator let us study rotations in its phase space. HARMONIC OSCILLATOR AND COHERENT STATES ln 0 N m.
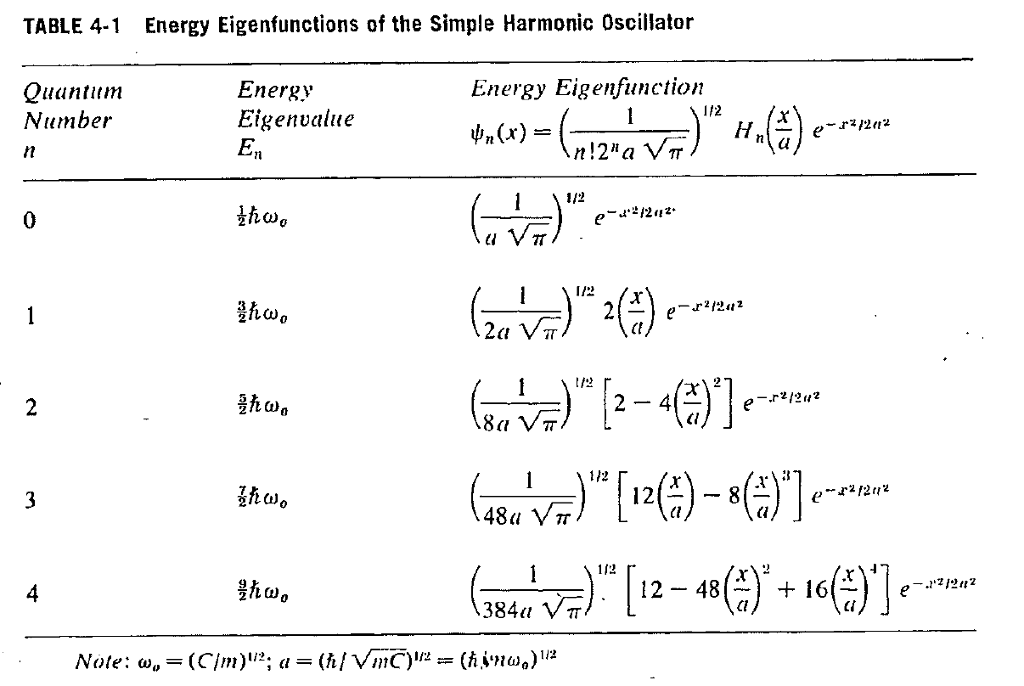
Because of the association of the wavefunction with a probability density it is necessary for the wavefunction to include a normalization constant Nv. Normalization of Simple Harmonic Oscillator wave function How to Normalize the wave functions of Simple Harmonic Oscillator. The Hamiltonian of the classical harmonic oscillator reads H p2 2 q2 2 1 we take the frequency and mass ω m 1. The normalized wavefunctions for the first four states of the harmonic oscillator are shown in Figure 561 and the corresponding probability densities are shown in Figure 562. Expanded around a minimum point x any potential can then be Taylor expanded as. In this section we will discuss the classical and quantum mechanical oscillator.
The normalization R1 1 dxj 0xj2 1 together with formula 2119 for Gaussian functions determines the normalization constant N2 r m.
The shape of the wave function is. The wavefunctions for the quantum harmonic oscillator contain the Gaussian form which allows them to satisfy the necessary boundary conditions at infinity. The harmonic oscillator is characterized by the Hamiltonian. So low that under the ground state is the potential barrier where the classically disallowed region lies. The normalization constant can be calculate easily using the integral formula of Laguerre polynomial. It represents the vibrational motion and is one of the few quantum-mechanical systems for which an exact solution is available.