
Rotation Matrix To Quaternion. The code Im using is. Then the rotation matrix corresponding to takes the following form. Quaternions are more compact than matrices to represent rotationsorientations Key operations. The matrix is special orthogonal which gives additional condition.
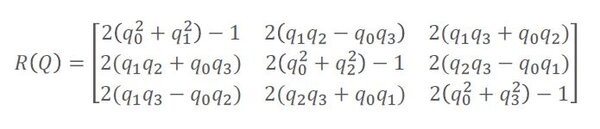
Calculate the trace of the matrix T from the equation. The converter can therefore also be used to normalize a rotation matrix or a quaternion. Following is a general rotation matrix obtained 1. The matrix is orthogonal. R Rfrom_quat 0 0 npsinnppi4 npcosnppi4 The rotation can be expressed in any of the other formats. Q and -q represent same rotation thus Other sign will be as follows.
We use unit length Quaternion to represent rotations.
A rotation may be converted back to a quaternion through the use of the following algorithm. Quat rotm2quat rotm converts a rotation matrix rotm to the corresponding unit quaternion representation quat. Qw 1 m00 m11 m22 2 qx m21 - m12 4 qw qy m02 - m20 4 qw. Conversion of rotation matrix to quaternion. Therefore By solving this Now lets calculate the sign. Quaternion q aa conversion error return q.